1. 三阶鱼
1.1. 原理
因为
- 存在 3 行 3 列
RegionLineParallel[1,3]、`RegionLinePerpendicular[1,3]:RegionLineParallel[n]之间互相平行RegionLinePerpendicular[n]之间互相平行RegionLinePerpendicular[n]垂直于RegionLinePerpendicular[m]RegionLineParallel[n]和RegionLinePerpendicular[m]相交于单元格Cell[nm]
- 对于候选数
X- 在行列
RegionLineParallel[1]中- 可填入数字
X的单元格仅限于Cell[11]、Cell[12]、Cell[13]
- 可填入数字
- 在行列
RegionLineParallel[2]中- 可填入数字
X的单元格仅限于Cell[21]、Cell[22]、Cell[23]
- 可填入数字
- 在行列
RegionLineParallel[3]中- 可填入数字
X的单元格仅限于Cell[31]、Cell[32]、Cell[33]
- 可填入数字
- 在行列
所以
- 在行列
RegionLinePerpendicular[1]中- 除了
Cell[11]、Cell[12]、Cell[13]的其他单元格- 必不填入数字
X
- 必不填入数字
- 除了
- 在行列
RegionLinePerpendicular[2]中- 除了
Cell[21]、Cell[22]、Cell[23]的其他单元格- 必不填入数字
X
- 必不填入数字
- 除了
- 在行列
RegionLinePerpendicular[3]中- 除了
Cell[31]、Cell[32]、Cell[33]的其他单元格- 必不填入数字
X
- 必不填入数字
- 除了
分析 9 格中数字
X的数量c:c >= 3 && c <= 3→c == 3
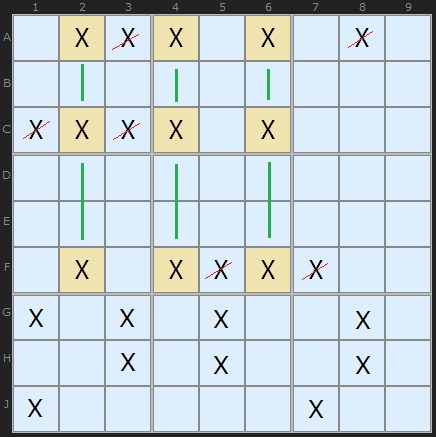
1.1.1. 技巧拓展
- [[二阶鱼]]:拓展分析行列区域的数量
1.2. 性质
1.2.1. 删除域
在[[二阶鱼#原理|原理]]的定义下,三阶鱼的删除域 指的是:
- 在行列
RegionLinePerpendicular[1]中- 除了
Cell[11]、Cell[12]、Cell[13]的其他单元格
- 除了
- 在行列
RegionLinePerpendicular[2]中- 除了
Cell[21]、Cell[22]、Cell[23]的其他单元格
- 除了
- 在行列
RegionLinePerpendicular[3]中- 除了
Cell[31]、Cell[32]、Cell[33]的其他单元格 故,结论可以简化为:
- 除了
- 三阶鱼的删除域:
- 必不填入数字
X
- 必不填入数字