1. 常见规则说明

1.1. 共边平行路

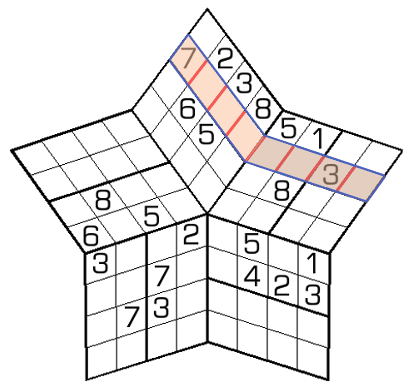
一个区域内，所有邻格的公共边互相平行

此类区域形似石板铺成的"路"

1.1.1. 棱

魔方中的共边平行路

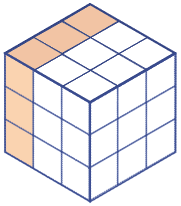
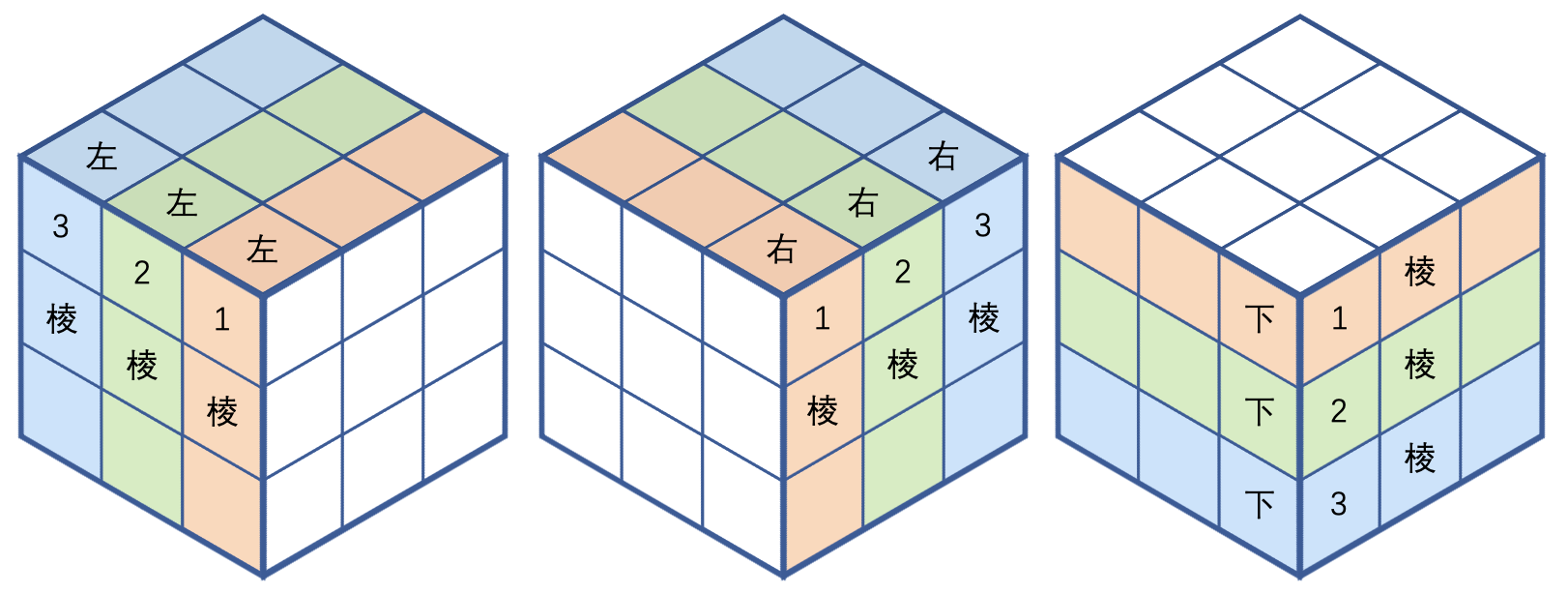
• 棱的编号
  • 方向：左，右，下
  • 数字：从中心点向外，分别为 1,2,3...

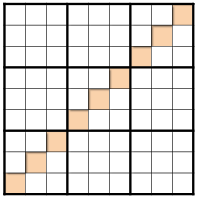
1.2. 上斜线

左下到右上的斜线区域

1.2.1. 上对角线

1.3. 下斜线

左上到右下的斜线区域

1.3.1. 下对角线

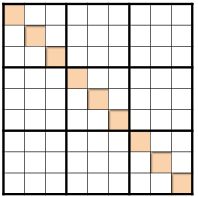
1.4. 对角线

经过天元，连接对角的区域。 主要包括：

• 上对角线
• 下对角线
• 弯对角线

1.4.1. 对角线约束

对角线上的数字不重复。

对于 9 阶数独，对角线满足：区域内1~9填充

1.4.2. 反对角线约束

对角线上的数字必重复。

对于 9 阶数独，反对角线满足：区域内仅有 3 种数字

1.5. 1to9填充

• 单一区域内填入 1-9
• 每个数字恰好出现 1 次。

1.6. 1toG填充

• 单一区域内填入 1-9A-G
• 每个字符恰好出现 1 次。

1.7. 1to8填充

• 单一区域内填入 1-8
• 每个数字恰好出现 1 次。

1.8. 1to6填充

• 单一区域内填入 1-6
• 每个数字恰好出现 1 次。

1.9. 9选6填充

• 在 1-9 中挑选 6 个数，单一区域内填入
• 每个数字恰好出现 1 次。

1.10. 全盘9选6填充

在 1-9 中挑选 6 个数，全盘仅出现这 6 种不同的数字。

1.11. 1to9不重复

• 单一区域内填入 1-9
• 每个数字出现 0 或 1 次。

1.12. 1to8不重复

• 单一区域内填入 1-8
• 每个数字出现 0 或 1 次。

1.13. 0to9不重复

• 单一区域内填入 0-9
• 每个数字出现 0 或 1 次。

1.14. 摩天楼

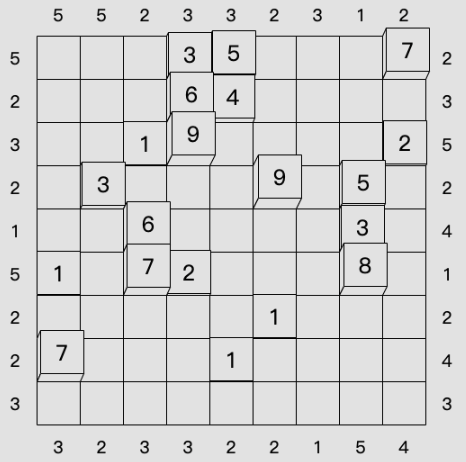
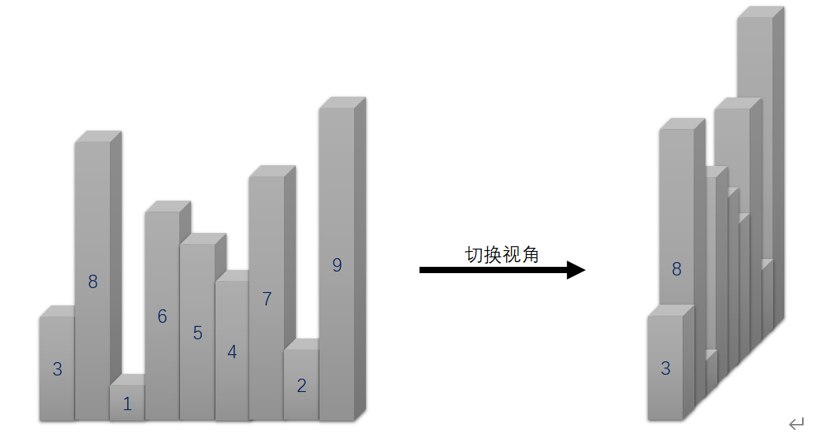
摩天楼规则需要一定的空间想象力，对以下内容进行对应理解：

• 数独盘面 → 平地
• 数独盘面内的数字 → 位于该位置上的楼的层数
• 9 宫摩天楼数独的解 → 平地上有 81栋高低不同的楼，其中 9 层高的楼有 9 栋，8 层高的楼有 9 栋，...，1 层高的楼也有 9 栋
• 摩天楼观测提示数 → 从提示数所在（观测位，观测方向）上，可以看到的楼栋数（即摩天楼观测数）
• 摩天和提示数 → 从提示数所在（观测位，观测方向）上，可以看到的部分楼，摩天和是这些楼的总层数

注意：存在高楼挡住矮楼，导致矮楼无法被看到的情况。

1.15. 摩天楼观测数

在摩天楼数独规则下，在指定（观测位，观测方向）上，可以看到 N 栋楼。摩天楼观测数是可以看到的楼栋数，即N。

1.16. 摩天和

在摩天楼数独规则下，在指定（观测位，观测方向）上，可以看到 N 栋楼。摩天和是这 N 栋楼的层数总和。

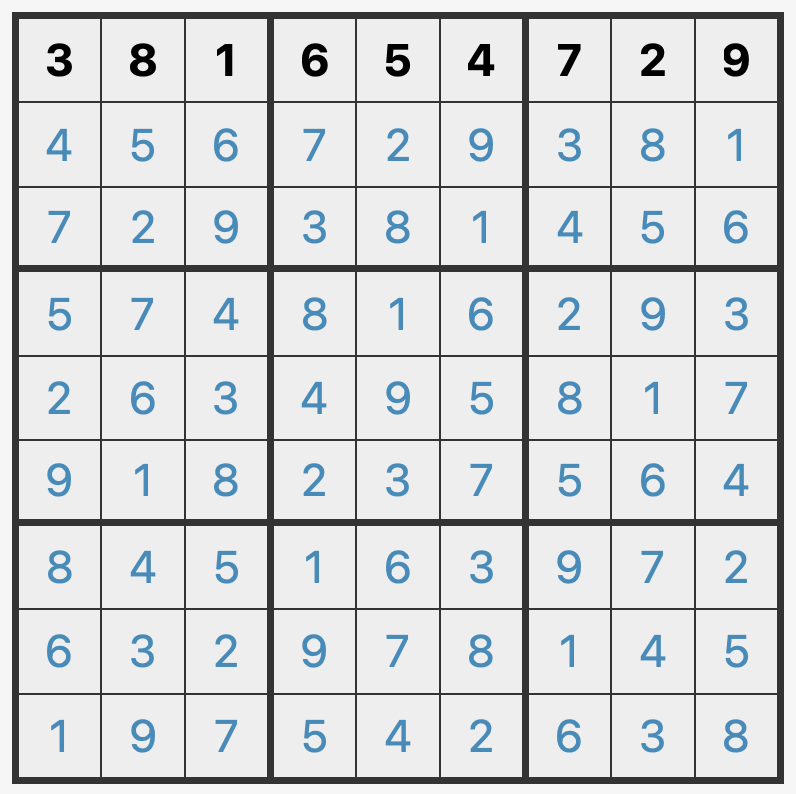
举例：

• 盘面信息：
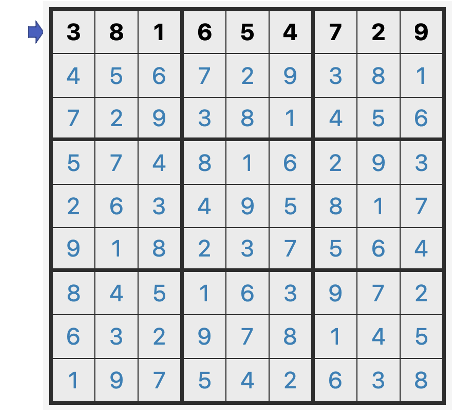
  • A 行的数字从左到右为：381654729
  • 
• 观测信息：
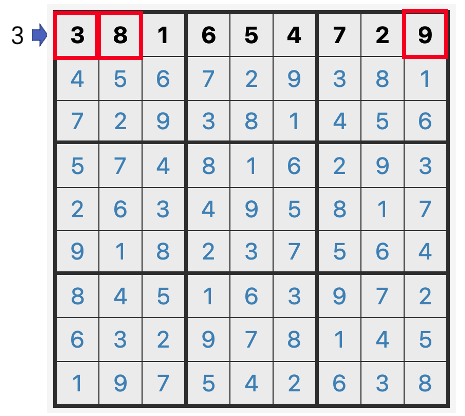
  • 从 A0（A1 左侧），向右观测
  • 
• 观测结果：可以看到 3 栋楼，分别是 3 层楼（A1）、8 层楼(A2)、9 层楼(A9)
  • A1(3层楼)：可以看到
  • A2(8层楼)：可以看到，8 层楼高于 3 层楼（8>3）
  • A3(1层楼)：无法看到，被 8 层楼挡住（1<8）
  • A4(6层楼)：无法看到，被 8 层楼挡住（6<8）
  • A5(5层楼)：无法看到，被 8 层楼挡住（5<8）
  • A6(4层楼)：无法看到，被 8 层楼挡住（4<8）
  • A7(7层楼)：无法看到，被 8 层楼挡住（7<8）
  • A8(2层楼)：无法看到，被 8 层楼挡住（2<8）
  • A9(9层楼)：可以看到，9 层楼高于 8 层楼（9>8）
  • 
• 结论：此例中，A0 位向右观测的
  • 摩天楼观测数 是 3
  • 摩天和 是 20=3+8+9
  • 

1.17. 邻格

两格拥有公共的点，则互为邻格。

对于标准 9 宫数独：

• A1,A9,I1,I9：有 3 个邻格
• {A,I}{2-8}，{B-H}{1,9}：有 5 个邻格
• {B-H}{2-8}：有 8 个邻格

1.17.1. 共边邻格

两格拥有公共的边，则互为共边邻格。

对于标准 9 宫数独：

• A1,A9,I1,I9：有 2 个共边邻格
• {A,I}{2-8}，{B-H}{1,9}：有 3 个共边邻格
• {B-H}{2-8}：有 4 个共边邻格

1.17.2. 对角邻格

两格拥有公共的点，但不存在公共的边，则互为对角邻格。

对于标准 9 宫数独：

• A1,A9,I1,I9：有 1 个对角邻格
• {A,I}{2-8}，{B-H}{1,9}：有 2 个对角邻格
• {B-H}{2-8}：有 4 个对角邻格

对角邻格 等价与 士步格

1.18. 连续

如果两格满足连续约束，说明这两格数字差为 1

1.18.1. 正交连续

如果共边邻格的公共边上存在标记，说明这两格数字差为 1

1.18.2. 斜连续

如果对角邻格的公共顶点上存在标记，说明这两格数字差为 1

1.19. 黑白点

如果共边邻格的公共边上存在黑白点标记，说明这两格数字大小满足：

• 黑点：两格数字是两格关系
• 白点：两格数字差为 1（即连续）

注意：1和2之间可能标记黑点，也可能标记白点

1.20. 数比

两格之间存在大小标志，说明这两个数字满足以下情况之一：

• =：两格数字相同
• >：开口方向格 大于 闭口方向格
• ⊿：斜边所在格 大于 直角方向格

1.21. 无缘

对于数字 A：

• 盘面内任意一个数字A，它的邻格都不是数字 A

在标准数独中，等价于：

• 盘面内任意一个数字A，它的对角邻格都不是数字 A
• 盘面内任意一个数字A，它的士步格都不是数字 A

1.22. 士步

两格的横向距离和纵向距离都是1，则互为士步格。

士步格等价与 对角邻格

1.23. 马步

两格的横向距离和纵向距离，一个是1，一个是2，则互为马步格。

对于标准 9 宫数独：

• A1,A9,I1,I9：有 2 个马步格
• {A,I}{2,8}，{B,H}{1,9}：有 3 个马步格
• B2,B8,H2,H8,{A,I}{3-7}，{C-G}{1,9}：有 4 个马步格
• {B,H}{3-7}，{C-G}{2,8}：有 6 个马步格
• {C-G}{3-7}：有 8 个马步格

1.23.1. 马步约束

两格互为马步格，且数字相同

1.23.2. 马步中心

互为马步的两格的中点

1.24. 象步

两格的横向距离和纵向距离都是2，则互为象步格。

对于标准 9 宫数独：

• {A,B,H,I}{1,2,8,9}: 有 1 个象步格
• {A,B,H,I}{3-7}，{C-G}{1,2,8,9}：有 2 个象步格
• {C-G}{3-7}：有 4 个象步格

1.25. 前X和

盘外提示数 S：当前位置向盘内看，第 1 格为X，前 X 格和为S

1.26. 边框和

盘外提示数 S: 当前位置向盘内看，前 3 格的和为 S

1.27. 奇偶星

• 区域：中心格 及其共边邻格，一般标记中心格
• 限制：中心格与其共边邻格奇偶性相反

引用：

• BiliBili：15：摩天楼数独

1.28. 骨牌

1 个骨牌占据 1 宫，每个骨牌包含 1-9 个骨牌点。

骨牌 1~9如下图所示：

1.28.1. 1to9骨牌填充

• 全盘填入 1-9 骨牌
• 每个骨牌恰好出现 1 次。

1.29. 耳语线

• 别名：German Whisper
• 限制：线上相邻数字的差值必须 ≥ 5

1.30. 连续区间线

• 别名：Renban
• 限制：线上的单元格满足连续区间限制

1.30.1. 连续区间限制

指定区域的数字恰好组成一个连续区间，但对顺序没有限制

1.31. 熵约束

1.31.1. 三格熵约束

三格满足熵约束，当且仅当 三格的数字恰好包含：

• 1 个小数 123
• 1 个中数 456
• 1 个大数 789

1.31.2. 2x2熵约束

2x2的 4 格满足熵约束，其中数字至少包含：

• 1 个小数 123
• 1 个中数 456
• 1 个大数 789

1.32. 熵线

• 别名：Entropic
• 限制：线的任何三个连续单元格都满足熵约束

1.33. 反熵线

• 别名：Anti-Entropic
• 限制：线的任何三个连续单元格都不满足熵约束

1.34. 模约束

三格满足模约束，当且仅当 三格的数字对 3 取模结果互异。 即恰好包含：

• 1 个 147（模 3 余 1）
• 1 个 258（模 3 余 2）
• 1 个 360（模 3 余 0）

1.35. 模线

• 别名：Modular
• 限制：线的任何三个连续单元格都满足模约束

1.36. 计算框

计算框是盘面中由"指示圈"框定的若干个单元格。 一般在"指示圈"左上角存在提示数。

1.37. 杀手框

杀手框是一种特殊的计算框，框内单元格数字各不相同。

• 别名：
  • Killer Cages

1.37.1. 杀手限制

• 框内格子数字各不相同
• 若存在提示数，即为框内单元格数字之和

1.38. 职业杀手框

职业杀手框是满足暗杀条件的杀手框

• 别名：Contract Killer Cages

1.38.1. 职业杀手限制

• 职业杀手框内，恰有 2 个单元格未被暗杀，其中
  • 上左格（上优先）值为R
  • 下右格（下优先）值为C
  • 该职业杀手框的暗杀对象为 R行C列单元格
• 职业杀手框的暗杀对象互不相同
• 若单元格被暗杀，其参与计算时值为 0

1.39. Psycho look-and-say cages

Psycho look-and-say cages 是盘面中由"指示圈"框定的若干个单元格。 在"指示圈"左上角存在提示数CX。

• 约定：
  • 指示圈包含单元格都是定位单元格
  • 每个定位单元格可通过以下方式指示唯一的目标单元格：
    • 目标单元格位于第定位单元格.数字宫
    • 目标单元格与定位单元格的宫内位置相同
• 限制：
  • 框内单元格数字各不相同
  • 提示数CX表示：所有目标单元格中恰有 C 个 X

1.40. 箭

• 箭尾：通过圆圈标记
• 箭身：通过线段标记
• 箭头：通过箭头符号标记

1.40.1. 箭限制

箭尾 = 箭身 + 箭头

1.41. 战争迷雾

• 别名：Fog of War

初始状态下，盘面内的提示标记被迷雾覆盖，无法观察。

当满足以下条件时展示，可驱散迷雾：

• 指示灯：可驱散当前格和周围邻格的迷雾
• 填入数字正确的单元格：可驱散周围邻格的迷雾